It’s Finally Time You Understand What a Quantum Bit Is Because It’s the Quantum Decade

Spread the love

In this blog post, you will learn what a quantum bit is from a quantum computing perspective, and you will learn about the Bloch sphere, which is an important visualization tool for examining the state of a qubit.

What is a qubit?

A quantum bit (qubit) is like a classical bit in classical computing because it is the most fundamental unit of information in quantum computing (Voorhoede, n.d.). A qubit can be in a state of |0⟩, which means the particle is spinning up and is like the 0 bit from a classical computing perspective. A qubit can also be in a state |1⟩, which means the particle is spinning down and represents the 1 bit from a classical computing perspective. The qubit can also be in a superposition of |0⟩ and |1⟩ where there is a probability $\alpha$ the qubit is in state |0⟩ and a probability $\beta$ the qubit is in state |1⟩, which is not possible in classical computing.

The qubit states |0⟩ and |1⟩ are represented in ket notation, which means they are vectors with complex numbers (“Bra-ket notation,” n.d.). The vector values for |0⟩ and |1⟩ can be observed in equations (1) and (2) respectively. In particular, the states |0⟩ and |1⟩ are the orthogonal z-basis states (Voorhoede, n.d.). The qubit can also be in a superposition of the states |0⟩ and |1⟩, and it can be expressed as a linear combination as seen in equation (3) where $\alpha$ and $\beta$ are the probability amplitudes (Menon & Ritwik, 2014; Voorhoede, n.d.). When the qubit is in superposition, the measurement of it causes it to collapse into a single state.

\|0⟩ $=\begin{bmatrix} 1\\0\end{bmatrix}$	(1)
\|1⟩ $=\begin{bmatrix} 0\\1\end{bmatrix}$	(2)
\| $\psi$ ⟩ = $\alpha$ \|0⟩ + $\beta$ \|1⟩	(3)

The Bloch Sphere

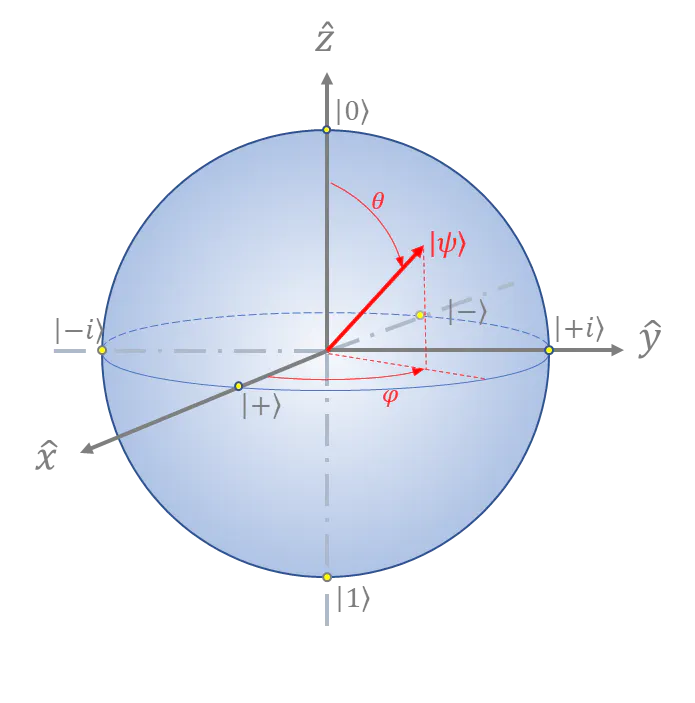
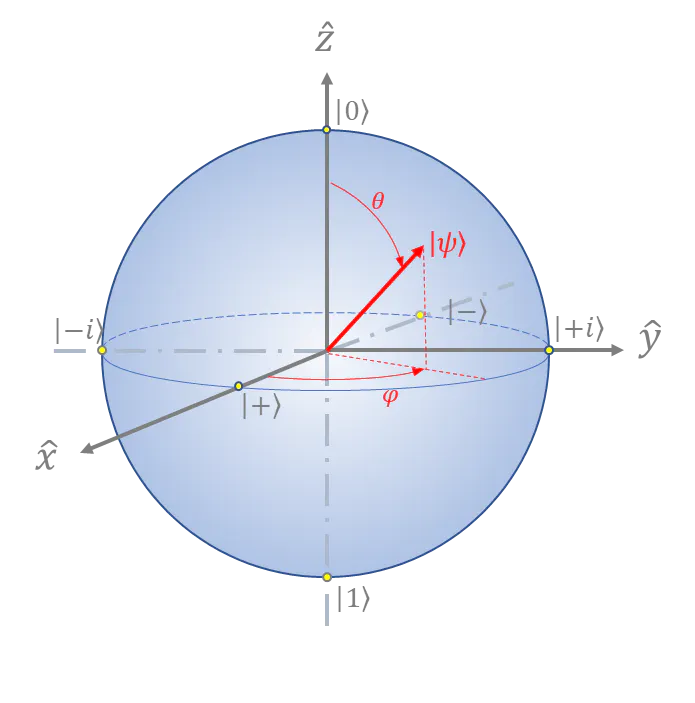
The Bloch sphere is a visual tool that helps one understand what is happening inside of a qubit, and a picture of the Bloch sphere can be seen in Figure 1 (“Quantum Computing,” 2021). An arbitrary state of a qubit on the Bloch sphere can be represented as equation (4) where $\theta$ represents latitude and $\phi$ represents the longitude on the Bloch sphere (Williams, 2011). One can convert the spherical polar coordinates to Euclidean coordinates by using equation (5) (Menon & Ritwik, 2014).

The orthogonal x-basis states are |+⟩ and |-⟩, and they are on the equator of the Bloch sphere along the x-axis, which can be observed in Figure 1 (Voorhoede, n.d.). The equations for |+⟩ and |-⟩ can be seen in equations (6) and (7) respectively (Voorhoede, n.d.).

The orthogonal y-basis states are |+i⟩ and |-i⟩, and they are on the equator of the Bloch sphere along the y-axis, which can be observed in Figure 1 (Voorhoede, n.d.). The equations for |+i⟩ and |-i⟩ can be seen in equations (8) and (9).

The orthogonal z-basis states and are on the north and south poles of the Bloch sphere respectively (Voorhoede, n.d.).

Figure 1

The Bloch Sphere

\| $\psi$ ⟩ = $\cos(\frac{\theta}{2})$ \|0⟩ + $e^{i\phi}\sin(\frac{\theta}{2})$ \|1⟩	(4)
$(x,y,z) = (\sin(\theta)\cos(\phi), \sin(\theta)\sin(\phi), \cos(\theta))$	(5)
\|+⟩ $= \frac{1}{\sqrt{2}}($ \|0⟩ + \|1⟩ $)$	(6)
\|-⟩ $= \frac{1}{\sqrt{2}}($ \|0⟩ – \|1⟩ $)$	(7)
\| $+i$ ⟩ $= \frac{1}{\sqrt{2}}($ \|0⟩ + $i$ \|1⟩ $)$	(8)
\| $-i$ ⟩ $= \frac{1}{\sqrt{2}}($ \|0⟩ – $i$ \|1⟩ $)$	(9)

Another important aspect of the Bloch sphere is phase, and there are two types of phase, which are global phase and relative phase (Ekert, 2021). Global phase is when the entire state of the qubit in equation (3) is multiplied by a complex number, which is irrelevant to the state of the qubit (Ekert, 2021). Relative phase is only when the |1⟩ state of equation (3) is multiplied by a complex number, and it essentially represents a rotation about the z-axis (Ekert, 2021).

In this blog post, you learned what a quantum bit is, and you learned what a Bloch sphere is.

Thanks for reading! For more blog posts just like this, subscribe, share, and buy me a coffee!

References

Bra-ket notation. (n.d.). Mathsisfun.com. Retrieved October 4, 2023, from https://www.mathsisfun.com/physics/bra-ket-notation.html

Ekert, A. [@ArturEkert]. (2021). IQIS Lecture 6.4 — Phase kick-back. Youtube. https://www.youtube.com/watch?v=iSCYkhkWVjw

Menon, P. S., & Ritwik, M. (2014). A Comprehensive but not Complicated Survey on Quantum Computing. IERI Procedia, 10(2014), 144–152.

Quantum Computing [@quantumcomputing2985]. (2021). EdX Bloch Sphere. Youtube. https://www.youtube.com/watch?v=Pfk_9RNQA5A

Voorhoede, D. (n.d.). What is a qubit? Quantum Inspire. Retrieved October 4, 2023, from https://www.quantum-inspire.com/kbase/what-is-a-qubit/

Williams, C. P. (2011). Quantum Gates. In Texts in Computer Science (pp. 51–122). Springer London.

It’s Finally Time You Understand What a Quantum Bit Is Because It’s the Quantum Decade

Subscribe